Các hệ thức lượng trong tam giác vuông [thường] chuẩn nhất

Hệ thức lượng trong tam giác vuông là một trong những kiến thức khá quan trọng trong trường phổ thông, để giúp các bạn nắm chắc hơn  nữa những kiến thức này, trong bài viết dưới đây chúng tôi sẽ cung cấp đầy đủ những kiến thức về các hệ thức lượng để giúp các em giải quyết các bài toán liên quan một cách nhanh chóng dễ dàng.

Tầm quan trọng của hệ thống kiến thức hệ thức lượng trong tam giác vuông.

Kiến thức về hệ thức lượng trong tam giác vuông sẽ được giới thiệu đến các em học sinh trông chương trình học của cấp học trung học cơ sở. Bắt đầu từ lớp 6 các em sẽ được tiếp cận dần với môn hình học với mảng kiến thức về hệ thức lượng trong tam giác, hệ thức lượng trong tam giác vuông. Khi nắm vững các kiến thức này các em sẽ vận dụng giải các bài toán tính diện tích tam giác, chứng minh hệ thức lượng trong tam giác vuông một cách nhanh chóng và dễ dàng. Chính thế với mặt bằng kiến thức chung mà nói thì Hệ thức lượng trong tam giác vuông là phần kiến thức rất quan trọng, nếu nắm chắc được nó, các em sẽ có thể ứng dụng vào nhiều dạng bài tập khác nhau ở cấp học trung học cơ sở và các cấp học cao hơn.

 Để giải được các bài toán có liên quan đến kiến thức về hệ thức lượng trong tam giác vuông, các em cần nắm vững khái niệm về tam giác vuông trước. Tam giác vuông đã quen thuộc với các em trong nhiều năm học, ngay từ khi học cấp 1 đã được làm quen với dạng hình học này.

Tam giác vuông được biết đến là dạng hình học tam giác có một góc vuông. Với các khái niệm về đường cao, cạnh huyền, cạnh bên các em cần hiểu rõ và nhận biết được. Chỉ khi nắm vững được các khái niệm này thì các em mới có thể ứng dụng và giải được các bài toán có liên quan đến hệ thức lượng trong tam giác vuông.

Bên cạnh đó, để làm được các bài toàn liên quan các em cũng cần nắm được các công thức tính toán khác nhau. Đây là việc bắt buộc nếu các em muốn tự mình giải bài tập tính toán cũng như bài tập chứng minh.

Các hệ thức lượng trong tam giác

Định lý cosin

Trong tam giác ABC bất kỳ với BC = a, CA = b, AB = c, ta có:

a² = b² + c² – 2b.c. cos A

b² = a² + c² – 2a.c. cos B

c² = a² + b² – 2a.b. cos C

Hệ quả

Áp dụng: Tính độ dài đường trung tuyến của tam giác.

Cho tam giác ABC có độ dài cạnh BC = a, CA = b, AB = c. Gọi m_a, m_b, m_c lần lượt là độ dài các đường trung tuyến vẽ từ đỉnh A, B, C của tam giác. Ta có:

Định lý Sin

Trong tam giác ABC bất kỳ với BC = a, CA = b, AB = c, và R là bán kính đường tròn ngoại tiếp. Ta có:

Công thức tính diện tích tam giác.

Với h_a, h_b, h_c lần lượt là đường cao của tam giác ABC vẽ từ các đỉnh A, B, C, ta có diện tích tam giác ABC:

Với, R là bán kính đường tròn loại tiếp, r là bán kính đường tròn nội tiếp, p là nửa chu vi của tam giác ABC, diện tích của tam giác ABC được tính theo một trong các công thức sau:

Công thức Heron còn có thể được viết lại như sau:

Kiến thức cơ bản về hệ thức lượng trong tam giác vuông

Kiến thức về hệ thức lượng trong tam giác vuông được hệ thống thành một loạt các công thức về các hệ thức về cạnh và đường cao trong tam giác vuông; các hệ thức về cạnh và góc trong tam giác vuông như sau:

Đối với Tam giác ABC vuông góc tại đỉnh A = 900, ta có công thức:

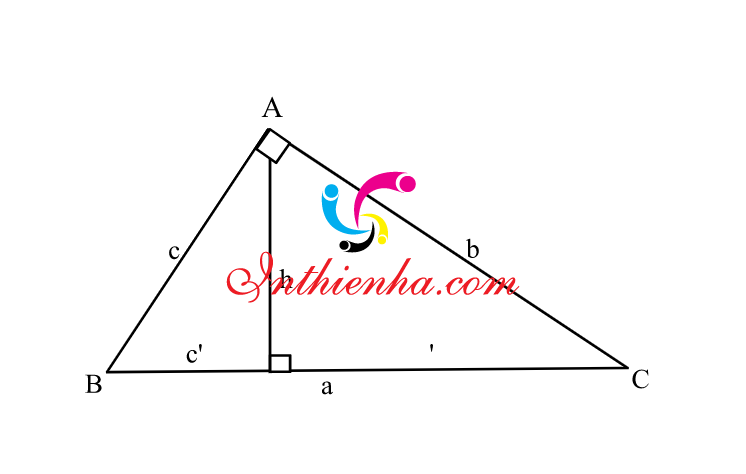
Ta có:

Công thức thức về cạnh và góc

b = a.SinB = a.CosC

c = a.SinC = a.CosB

b= c.TgB= c.CotgC

c = b.TgC = b.CotgB

Để giải được các bài toán về hệ thức lượng trong tam giác vuông thì không còn cách nào khác là các em buộc phải học thuộc lòng các công thức vừa được chia sẻ nha. Các công thức này chính là chìa khóa giúp các em giải bài tập một cách nhanh chóng và hiệu quả nhất. Với các công thức này, các em có thể ứng dụng vào giải các bài tập hệ thức lượng trong tam giác vuông lớp 9 sách giáo khoa và sách bài tập, một các dễ dàng. Còn với những bài toán cao cấp hơn thì các em có thể tham khảo cách giải mẫu trước rồi từ đó ứng dụng vào làm các bài toán tương tự thì các em hoàn toàn có thể làm chủ mảng kiến thức này.

Những lưu ý khi giải các dạng toán hệ thức lượng trong tam giác

Mặc dù đã nắm được công thức một cách nhuần nguyễn rồi nhưng khi giải các bào toán về hệ thức lượng trong tam giác vuông các em sẽ cần giải quyết một số dạng toán từ cơ bản đến nâng cao như: tính diện tích tam giác, chứng minh hệ thức lượng trong tam giác vuông, các bài toán biến đổi hệ thức nâng cao…không thể nôn nóng đốt cháy giai đoạn được nha

 Về áp dụng công thức tính hệ thức lượng trong tam giác để giải bài toán tính diện tích

Trước tiên cần xác định được chiều cao của tam giác. Khi một bài toán không nêu rõ chiều cao của tam giác, em có thể kẻ thêm hình phụ là đường cao ứng với cạnh huyền từ đó mới tính ra các tài liệu khác phục vụ cho công việc tính diện tích. Nói chung dạng toán này khá đơn giản, chỉ cần áp dụng công thức là xong

Còn một cách nữa là để tính diện tích tổng các em cũng có thể chia tam giác thành các tam giác nhỏ khác nhau với đường cao để tính diện tích tam giác. Cách này có thể áp dụng với các bài toán hệ thức lượng trong tam giác cân, tam giác vuông, tam giác thường.

Với các bài toán chứng minh và bài toán biến đổi 

Giải bài toán dạng này, trước tiên các em cần kẻ hình chuẩn, vẽ hình tốt với các góc hình dễ nhìn, các em sẽ dễ dàng nhìn ra điểm đặc biệt trong bài toán sau đó áp dụng công thức là có thể giải được, lưu ý làm càng nhiều thì càng nhuần nhuyễn

Bài tập hệ thức lượng trong tam giác vuông được ứng dụng rất nhiều trong thực tế khi đo chiều cao của tòa nhà, vật thể cao… chứ không chỉ là lý thuyết suông trong trường phổ thông, chính vì vậy, nếu học tốt, các em sẽ thấy rất thú vị khi mình có thể áp dụng vào đời sống. Chúc các em học tốt.